알고리즘/백준
[백준][C++] 2887: 행성 터널
KANTAM
2023. 12. 26. 19:40
문제
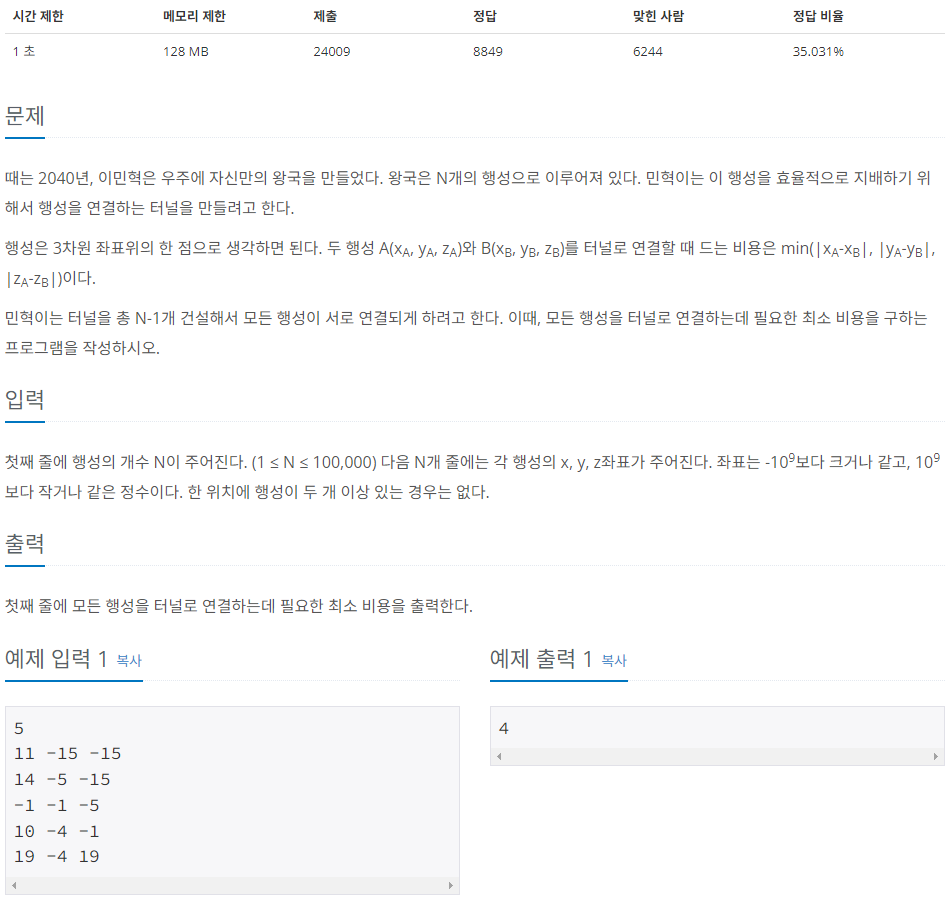
2887번: 행성 터널
첫째 줄에 행성의 개수 N이 주어진다. (1 ≤ N ≤ 100,000) 다음 N개 줄에는 각 행성의 x, y, z좌표가 주어진다. 좌표는 -109보다 크거나 같고, 109보다 작거나 같은 정수이다. 한 위치에 행성이 두 개 이
www.acmicpc.net
풀이
최소 스패닝 트리, 크루스칼 알고리즘, 정렬
문제에서 행성 사이의 가중치 후보는 x좌표, y좌표, z좌표의 차의 절댓값이다. 행성의 수는 최대 100,000개 이므로 각 행성에서 다른 모든 행성에 대해 탐색한다면 시간초과와 메모리 초과가 발생한다.
그러므로, 행성 사이의 가중치 후보를 줄여서 계산해야 한다. 행성 사이의 거리는 x, y, z 좌표 차이 중 최솟값이므로, 각 좌표를 나눠서 처리한다.
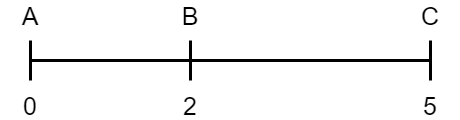
A, B, C 행성의 x좌표가 위처럼 되어있다고 하자. A - B, B - C를 잇는 경우가 A - C, C - B를 잇는 경우보다 가중치가 적다. 그러므로 행성 사이의 가중치 후보는 행성 바로 옆의 행성과의 거리가 된다.
위를 계산하기 위해서 x, y, z 좌표를 따로 입력받고 정렬하여 각 행성에서 각 좌표에 대해 바로 옆 행성과의 거리를 구하고 간선으로 저장한다. 저장한 간선으로 크루스칼 알고리즘을 실시하여 최소 가중치를 구한다. 이렇게 하면 각 행성마다 탐색해야할 행성의 수가 2개로 줄어들며, 가중치 후보가 6개로 줄어들어 시간초과와 메모리 초과가 발생하지 않는다.
코드
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
typedef struct
{
int node;
int dist;
}node_data;
typedef struct
{
int n1;
int n2;
int dist;
}edge;
vector<node_data> node_x;
vector<node_data> node_y;
vector<node_data> node_z;
vector<edge> edges;
int parent[100000];
int getParent(int n)
{
if (n == parent[n])
{
return n;
}
return getParent(parent[n]);
}
bool cycle(int n1, int n2)
{
n1 = getParent(n1);
n2 = getParent(n2);
return n1 == n2;
}
void Union(int n1, int n2)
{
int p1 = getParent(n1);
int p2 = getParent(n2);
if (p1 < p2)
{
parent[p2] = p1;
}
else
{
parent[p1] = p2;
}
}
bool compareNodeData(node_data a, node_data b)
{
return a.dist < b.dist;
}
bool compareEdge(edge a, edge b)
{
return a.dist < b.dist;
}
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(NULL);
cout.tie(NULL);
int N;
cin >> N;
for (int i = 0; i < N; ++i)
{
int x, y, z;
cin >> x >> y >> z;
// x, y, z 좌표를 모두 따로 입력받는다.
node_x.push_back({ i, x });
node_y.push_back({ i, y });
node_z.push_back({ i, z });
}
// 좌표 위치 순으로 정렬
sort(node_x.begin(), node_x.end(), compareNodeData);
sort(node_y.begin(), node_y.end(), compareNodeData);
sort(node_z.begin(), node_z.end(), compareNodeData);
for (int i = 1; i < N; ++i)
{
// 크루스칼 알고리즘은 최소 거리의 간선을 선택하는 알고리즘이다.
// 최소 거리가 될 수 있는 간선의 후보들은 한 노드와 바로 옆의 노드와의 거리가 된다.
// A -> B -> C 순으로 x좌표가 위치해있을 때,
// A -> C로 가는 거리는 A -> B -> C로 가는 거리와 같으므로, 굳이 후보에 넣지 않아도 무방하다.
edges.push_back({ node_x[i - 1].node, node_x[i].node, node_x[i].dist - node_x[i - 1].dist });
edges.push_back({ node_y[i - 1].node, node_y[i].node, node_y[i].dist - node_y[i - 1].dist });
edges.push_back({ node_z[i - 1].node, node_z[i].node, node_z[i].dist - node_z[i - 1].dist });
}
// 크루스칼 알고리즘 실시
sort(edges.begin(), edges.end(), compareEdge);
for (int i = 0; i < N; ++i)
{
parent[i] = i;
}
int answer = 0;
for (auto edge : edges)
{
if (!cycle(edge.n1, edge.n2))
{
Union(edge.n1, edge.n2);
answer += edge.dist;
}
}
cout << answer;
return 0;
}
