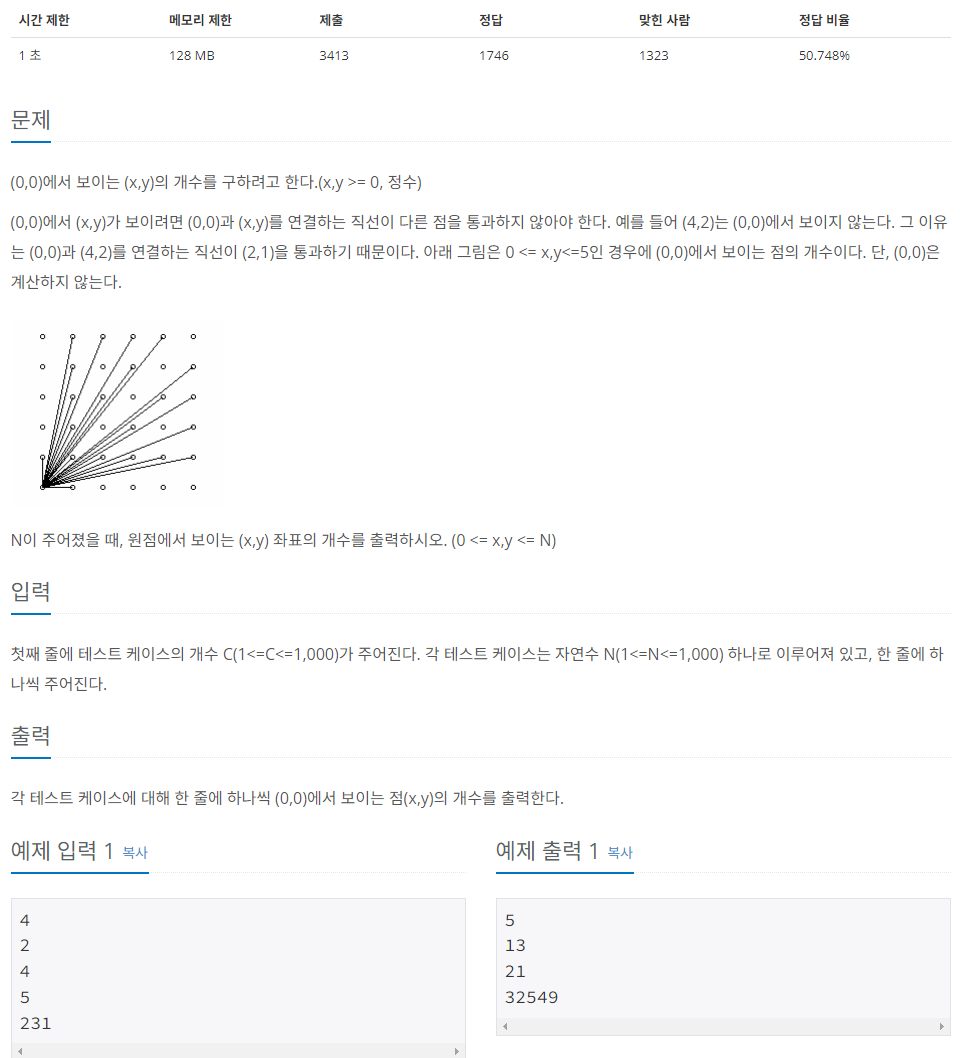
문제
2725번: 보이는 점의 개수
첫째 줄에 테스트 케이스의 개수 C(1<=C<=1,000)가 주어진다. 각 테스트 케이스는 자연수 N(1<=N<=1,000) 하나로 이루어져 있고, 한 줄에 하나씩 주어진다.
www.acmicpc.net
풀이
유클리드 호제법, 누적 합
[백준][C++] 10166: 관중석
문제 10166번: 관중석 KOI 공연장의 관중석에는 가운데에 있는 무대를 중심으로 반지름이 자연수인 동심원(중심이 같은 여러 원들) 위에 다음과 같이 좌석들이 배치되어 있다. 반지름이 1인 원 위
kantatatam.tistory.com
위의 문제처럼 좌표를 기약분수로 표현하여, 중복되지 않았을 때, 답으로 추가하여 구하려고 했지만 시간초과가 발생하였다.
N에서 보이는 점은 N - 1에서 보이는 점을 포함하므로, N에서 보이는 점은 (N - 1에서 보이는 점) + (N에서만 보이는 점)이다. N에서만 보이는 점은 x가 N이거나, y가 N인 줄에서 보이는 점이다. 해당 점에서의 최대공약수가 1이라면, 해당 점은 N - 1까지 가려지지 않은 점이다.
코드
#include <iostream>
using namespace std;
int nums[1001];
int gcd(int a, int b)
{
if (a < b)
{
swap(a, b);
}
int temp;
while (b != 0)
{
temp = a % b;
a = b;
b = temp;
}
return a;
}
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(NULL);
cout.tie(NULL);
int C;
cin >> C;
nums[1] = 3;
int num = 0;
for (int i = 2; i <= 1000; ++i)
{
// i에서 보이는 점은 i - 1에서 보이는 점을 포함한다.
nums[i] = nums[i - 1];
for (int j = 1; j < i; ++j)
{
// i, j의 최대공약수가 1이라면 i - 1까지 가려지지 않은 점이다.
int GCD = gcd(i, j);
if (GCD == 1)
{
// 기울기가 1인 선분과 대칭하므로, 2씩 추가
nums[i] += 2;
}
}
}
while (C--)
{
int N;
cin >> N;
cout << nums[N] << '\n';
}
return 0;
}
'알고리즘 > 백준' 카테고리의 다른 글
| [백준][C++] 2217: 로프 (0) | 2024.01.26 |
|---|---|
| [백준][C++] 5585: 거스름돈 (1) | 2024.01.25 |
| [백준][C++] 10166: 관중석 (0) | 2024.01.23 |
| [백준][C++] 1188: 음식 평론가 (1) | 2024.01.22 |
| [백준][C++] 2436: 공약수 (0) | 2024.01.21 |
