문제
1368번: 물대기
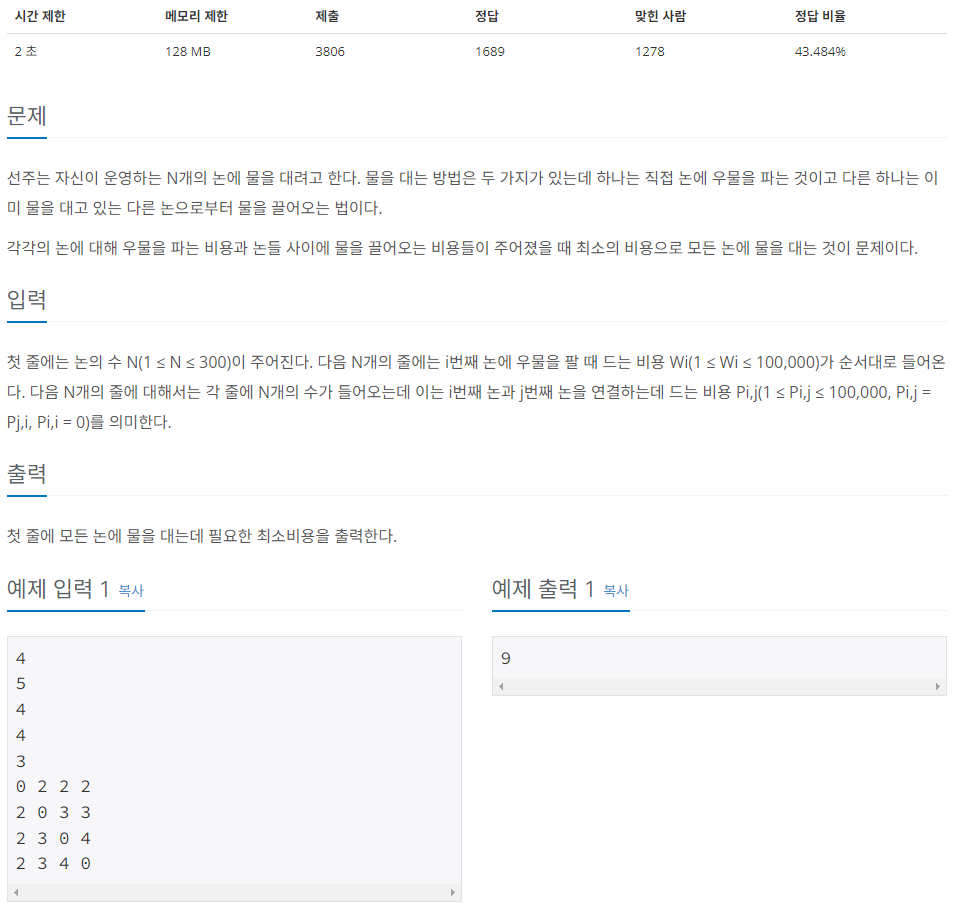
첫 줄에는 논의 수 N(1 ≤ N ≤ 300)이 주어진다. 다음 N개의 줄에는 i번째 논에 우물을 팔 때 드는 비용 Wi(1 ≤ Wi ≤ 100,000)가 순서대로 들어온다. 다음 N개의 줄에 대해서는 각 줄에 N개의 수가 들어
www.acmicpc.net
풀이
최소 스패닝 트리, 크루스칼 알고리즘
노드에 물을 받을 수 있는 경우는 노드에 우물을 파거나, 물이 들어오는 노드와 연결시키는 것이다. 이 두가지를 하나의 그래프로 표현해야 한다. 우물을 파는 경우를 하나의 노드로 표현하여 한 노드에서 우물을 파는 비용을 해당 노드와 우물을 파는 노드와의 간선의 거리로 표현하여 연결할 수 있다.
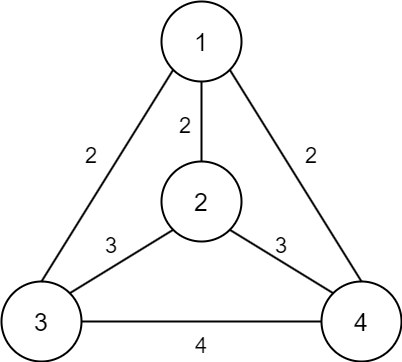
기존에는 그래프가 위처럼 되어있다. 여기에 우물 노드를 추가하면 밑의 그래프처럼 표현할 수 있다.
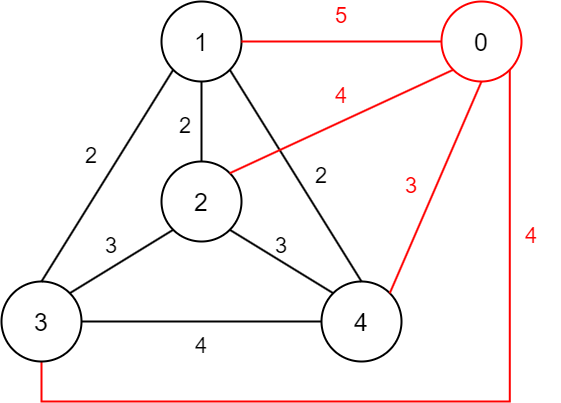
0번 노드가 우물을 파는 경우에 해당하며 각 노드에서의 거리가 우물을 파는 비용을 뜻한다. 위의 그래프에서 크루스칼 알고리즘을 실시하면, 0번 노드(우물)가 포함되면서 최소 스패닝 트리가 완성된다.
코드
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
typedef struct
{
int n1;
int n2;
int dist;
}edge;
vector<edge> edges;
int parent[301];
bool compare(edge a, edge b)
{
return a.dist < b.dist;
}
int getParent(int n)
{
if (n == parent[n])
{
return n;
}
return getParent(parent[n]);
}
bool cycle(int n1, int n2)
{
n1 = getParent(n1);
n2 = getParent(n2);
return n1 == n2;
}
void Union(int n1, int n2)
{
int p1 = getParent(n1);
int p2 = getParent(n2);
if (p1 < p2)
{
parent[p2] = p1;
}
else
{
parent[p1] = p2;
}
}
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(NULL);
cout.tie(NULL);
int N;
cin >> N;
// 우물을 파는 경우엔 0번 노드와 연결시킨다.
for (int i = 0; i < N; ++i)
{
int temp;
cin >> temp;
edges.push_back({ i + 1, 0, temp });
}
for (int i = 0; i < N; ++i)
{
for (int j = 0; j < N; ++j)
{
int temp;
cin >> temp;
// 0번 노드는 우물을 파는 경우이므로 각 노드에 +1을 처리하여 간선에 넣는다.
if (i != j)
{
edges.push_back({ i + 1, j + 1, temp });
}
}
}
// 크루스칼 알고리즘 실시
sort(edges.begin(), edges.end(), compare);
for (int i = 0; i <= N; ++i)
{
parent[i] = i;
}
int answer = 0;
for (auto edge : edges)
{
if (!cycle(edge.n1, edge.n2))
{
Union(edge.n1, edge.n2);
answer += edge.dist;
}
}
cout << answer;
return 0;
}
'알고리즘 > 백준' 카테고리의 다른 글
| [백준][C++] 1010: 다리 놓기 (1) | 2023.12.31 |
|---|---|
| [백준][C++] 1944: 복제 로봇 (0) | 2023.12.29 |
| [백준][C++] 13418: 학교 탐방하기 (1) | 2023.12.27 |
| [백준][C++] 2887: 행성 터널 (1) | 2023.12.26 |
| [백준][C++] 10432: 전기가 부족해 (0) | 2023.12.25 |
문제
1368번: 물대기
첫 줄에는 논의 수 N(1 ≤ N ≤ 300)이 주어진다. 다음 N개의 줄에는 i번째 논에 우물을 팔 때 드는 비용 Wi(1 ≤ Wi ≤ 100,000)가 순서대로 들어온다. 다음 N개의 줄에 대해서는 각 줄에 N개의 수가 들어
www.acmicpc.net

풀이
최소 스패닝 트리, 크루스칼 알고리즘
노드에 물을 받을 수 있는 경우는 노드에 우물을 파거나, 물이 들어오는 노드와 연결시키는 것이다. 이 두가지를 하나의 그래프로 표현해야 한다. 우물을 파는 경우를 하나의 노드로 표현하여 한 노드에서 우물을 파는 비용을 해당 노드와 우물을 파는 노드와의 간선의 거리로 표현하여 연결할 수 있다.

기존에는 그래프가 위처럼 되어있다. 여기에 우물 노드를 추가하면 밑의 그래프처럼 표현할 수 있다.

0번 노드가 우물을 파는 경우에 해당하며 각 노드에서의 거리가 우물을 파는 비용을 뜻한다. 위의 그래프에서 크루스칼 알고리즘을 실시하면, 0번 노드(우물)가 포함되면서 최소 스패닝 트리가 완성된다.
코드
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
typedef struct
{
int n1;
int n2;
int dist;
}edge;
vector<edge> edges;
int parent[301];
bool compare(edge a, edge b)
{
return a.dist < b.dist;
}
int getParent(int n)
{
if (n == parent[n])
{
return n;
}
return getParent(parent[n]);
}
bool cycle(int n1, int n2)
{
n1 = getParent(n1);
n2 = getParent(n2);
return n1 == n2;
}
void Union(int n1, int n2)
{
int p1 = getParent(n1);
int p2 = getParent(n2);
if (p1 < p2)
{
parent[p2] = p1;
}
else
{
parent[p1] = p2;
}
}
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(NULL);
cout.tie(NULL);
int N;
cin >> N;
// 우물을 파는 경우엔 0번 노드와 연결시킨다.
for (int i = 0; i < N; ++i)
{
int temp;
cin >> temp;
edges.push_back({ i + 1, 0, temp });
}
for (int i = 0; i < N; ++i)
{
for (int j = 0; j < N; ++j)
{
int temp;
cin >> temp;
// 0번 노드는 우물을 파는 경우이므로 각 노드에 +1을 처리하여 간선에 넣는다.
if (i != j)
{
edges.push_back({ i + 1, j + 1, temp });
}
}
}
// 크루스칼 알고리즘 실시
sort(edges.begin(), edges.end(), compare);
for (int i = 0; i <= N; ++i)
{
parent[i] = i;
}
int answer = 0;
for (auto edge : edges)
{
if (!cycle(edge.n1, edge.n2))
{
Union(edge.n1, edge.n2);
answer += edge.dist;
}
}
cout << answer;
return 0;
}
'알고리즘 > 백준' 카테고리의 다른 글
| [백준][C++] 1010: 다리 놓기 (1) | 2023.12.31 |
|---|---|
| [백준][C++] 1944: 복제 로봇 (0) | 2023.12.29 |
| [백준][C++] 13418: 학교 탐방하기 (1) | 2023.12.27 |
| [백준][C++] 2887: 행성 터널 (1) | 2023.12.26 |
| [백준][C++] 10432: 전기가 부족해 (0) | 2023.12.25 |
